Law of Large Numbers

When cleaning out my Google Drive, I came across a book from my freshman year of college called Street Fighting Mathematics: The Art of Educated Guessing and Problem Solving by Sanjoy Mahajan. The general premise behind the book is that most people need to understand general principles of math in order to live their lives, but they don’t need to know all the theory behind it. Instead, it’s better to develop an intuition about the way things work and make educated guesses from there. This aligns well with what I’m trying to accomplish in this blog, and it made me rethink how I could explain concepts without using any equations. Here’s my first attempt: the Law of Large Numbers.

If you’ve been following me for awhile, you know that I’ve talked before about the Law of Large Numbers and why it’s important for understanding the quality of scientific studies. According to Wikipedia:

In probability theory, the law of large numbers (LLN) is a mathematical law that states that the average of the results obtained from a large number of independent random samples converges to the true value, if it exists.

Another way to say it - the more data points you have, the more accurate your understanding of the data is.

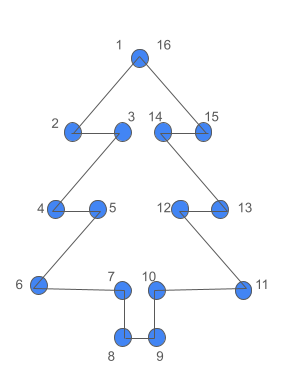
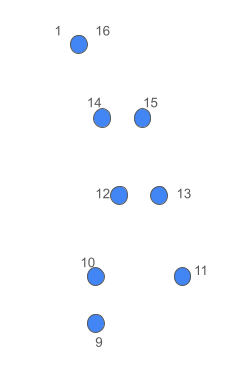
Rather than explaining this in terms of equations as I’ve done before, I want to embrace the street-fighting ethos and instead consider the concept of connect-the-dots. Connect-the-dots is a puzzle game in which you are given a paper with multiple numbered dots. Your job is to connect them in order to reveal the picture. Let’s say your paper is damaged, so you can only see some of the dots:

You know that your picture is incomplete, so you need to guess at where the lines should go. For example, would dot number 3 be exactly in between dots 2 and 4? Or would it be off to the left or the right? There are lots of ways you could connect these dots, like this:

Or this:

Or even this:

You’d have to use your knowledge of the puzzle to decide how best to fill in those gaps, but you’d still be guessing. What if you had the full, original puzzle instead?

While there are still multiple ways to connect these dots, this lends itself much more naturally to a single solution, especially when we use our domain knowledge of connect-the-dots to assume that the end result is supposed to be a recognizable object:

The same holds true in mathematics - the more data points you have, the more likely you are to be converging on the true value. And if you have enough points and enough knowledge of your domain, you can be more confident in your result. However, Wikipedia specifies the type of samples we need - “independent” and “random”. In other words, the samples should come from all over the space we’re investigating and they shouldn’t depend on each other. This translates to our example well. Imagine we only have half the page:

You can make a pretty good guess at the right side of the picture, but what about the left? Maybe we can figure it out that it’s supposed to be a tree, but it would still be just a guess. What if it was supposed to be a house with multiple eaves? Or the side profile of a man with a big nose and chin? It’s impossible to say for sure without getting more of the dots. The Law of Large Numbers says that you’ll be more confident if you got more dots on the left side of the picture.